lunes, 23 de marzo de 2015
jueves, 19 de marzo de 2015
Movimiento periódico y movimiento armónico simple
Rotación de la tierra, traslación de la luna, el péndulo de un reloj, el
movimiento de una masa que oscila
suspendida de un resorte, el movimiento de una partícula colocada sobre un
disco que está girando, entre otros.
Estudiaremos un caso particular del movimiento periódico. Consideremos una masa que se encuentra atada a un resorte, ambos cuerpos se encuentran
sobre un plano horizontal, tal como se observa en la gráfica. Despreciemos el rozamiento entre la fuerza horizontal y
la masa para simplificar su estudio.
Sí ejercemos sobre la masa m una fuerza F que la separe de su posición de equilibrio, se observa que el resorte
ejerce una fuerza en sentido contrario (- F) que tiende a
llevar la masa m a su posición de
equilibrio.
Sí
soltamos la masa m dejándola libre,
la fuerza recuperadora del
resorte la llevará hacia la posición de
equilibrio, debido a la inercia; se puede observar
que la masa no se detiene en el punto de equilibrio, si no que se sigue
moviendo hacia la izquierda. Desde el momento en que la masa m pasa por el
punto de equilibrio
(X = 0), la fuerza recuperadora - F
cambia de sentido y ahora se dirige hacia la derecha. Debido a la fuerza
recuperadora, la masa m se detiene
y su velocidad cambia de sentido
moviéndose hacia la derecha, hasta pasar nuevamente por el punto de equilibrio.
De esta forma el movimiento continúa en forma periódica.
Es
un movimiento periódico producido
por una fuerza recuperadora. Para
definir el MAS, necesitamos hablar de las fuerzas recuperadoras, con la
siguiente actividad se entenderá el fundamento de dichas fuerzas.
En
la siguiente gráfica se ilustra las
diferentes deformaciones que sufre un resorte cuando de él suspendemos
diferentes masas, supongamos que cada masa suspendida tiene un valor de 0,1 Kg.
De
la gráfica anterior podemos construir
una tabla de fuerza en función de la deformación
del resorte (X) medida en
metros. Debemos tener en cuenta que la X no representa la longitud del resorte, sino su deformación que es igual a la longitud
que adquiere el resorte menos su
longitud inicial, es decir:
De la misma forma se obtienen las
demás fuerzas y deformaciones.
Con
la información anterior podemos construir una gráfica de la fuerza F en función de la deformación X, así:
De
la gráfica se observa que la curva
que se obtuvo es una recta que pasa
por el origen de coordenadas, lo que
significa que las dos variables son directamente
proporcionales, por lo tanto la constante
de proporcionalidad K se obtiene dividiendo F (variable independiente) sobre X (variable dependiente), es decir:
El signo de la fuerza
recuperadora es negativo debido a
que F es contraria al movimiento del cuerpo y trata de llevarlo a su posición
de equilibrio. Todo esto se debe a la tercera ley de Newton (Ley de acción y reacción).
Ejemplo
¿Cuál es la K de un resorte, sí al ejercer sobre él una fuerza F = 12 N se deforma 20 Centímetros? ¿Cuál es
la masa m que se ata al resorte, para que sufra esta deformación?
miércoles, 18 de marzo de 2015
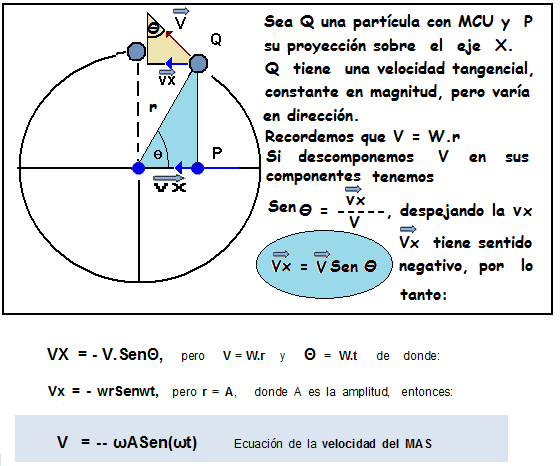
Ecuaciones del MAS: Elongación, velocidad y aceleración.
Para deducir las ecuaciones del MAS utilizaremos un modelo geométrico que consiste en proyectar en
uno de los ejes, el movimiento que
sigue una partícula Q (MCU). De la siguiente gráfica podemos
hacer el siguiente análisis:
Para t = 0 la partícula Q coincide en la posición A
con la partícula P que es su
proyección. Cuando Q ha recorrido un
cuarto de la circunferencia, P se
encuentra en el punto de equilibrio. Cuando Q ha recorrido media circunferencia, Q y P coinciden en el punto B. Cuando Q recorre ¾ de la circunferencia, P se encuentra en el punto de equilibrio. Finalmente se completa la
trayectoria cuando P y Q
vuelven a su punto inicial, que es la posición
A.
En el MAS se
utilizan algunos términos de gran importancia:
- Oscilación: Es el movimiento efectuado por una partícula hasta volver a su posición inicial, recorriendo todos los puntos de su trayectoria. En la gráfica anterior la oscilación es el movimiento efectuado por la partícula P que parte de A, llega a B y se regresa nuevamente a A.
- Período: Es el tiempo que tarda la partícula en hacer una oscilación completa, se representa por la letra T y se mide en segundos.
- Frecuencia: Es el número de oscilaciones que realiza una partícula en la unidad de tiempo. Se representa por la letra f y se expresa en oscilaciones por segundo, pero operacionalmente se emplea:
Seg -1 = Hertz (Hz)
- Punto de equilibrio: Punto de la trayectoria en el cual, la fuerza recuperadora es nula (vale cero). En la gráfica anterior es el punto O.
- Puntos de retorno: Son los dos extremos de la trayectoria en los cuales el movimiento cambia de sentido.
- Elongación: Es el desplazamiento de la partícula en un instante dado, referido al punto de equilibrio. Se representa por la letra X y se mide en metros o centímetros.
- Amplitud: Es la máxima elongación que puede tener la partícula, se representa por la letra A y se mide en metros o centímetros. La distancia entre los dos puntos de retorno es 2A.
Ecuación de
elongación Si consideramos el eje horizontal, vemos que r es la máxima elongación, por lo tanto:
Ecuación de la
velocidad
Ecuación de la aceleración
martes, 17 de marzo de 2015
Energías del MAS
Sí hay una masa que se encuentra atada a un resorte, es
necesario que para dar inicio al movimiento, hacer un trabajo sobre la masa m con el fin de
desplazarla de su posición de equilibrio.
Este trabajo W
se convierte en un tipo de energía que llamaremos ENERGIA POTENCIAL ELASTICA y que depende de la amplitud que le demos al movimiento.
Cuando dejamos la masa
m libre, ésta comienza a adquirir velocidad, ENERGIA CINETICA a costa de la energía potencial elástica inicial.
Cuando la masa m pasa por el punto de equilibrio X = 0, toda la energía
inicial, que es energía potencial
elástica se convierte en energía cinética,
ya que en este punto no existe energía
potencia elástica, ya que X = 0. Después la masa comienza a
perder energía cinética porque la
fuerza recuperadora F está dirigida
en sentido contrario a la velocidad,
produciendo una aceleración retardatriz;
de esta forma la energía potencial elástica se recupera cuando la masa m
llega al punto de retorno. De esta forma el movimiento se repite nuevamente, ya
que el resorte busca volver a su
estado inicial.
Para analizar las energías existentes, es necesario que
miremos la siguiente figura:
Como inicialmente
el resorte se deforma una longitud igual a la AMPLITUD A
del movimiento, entonces encontramos que el trabajo realizado y la energía
potencial inicial del sistema masa-resorte son:
En la siguiente animación se podrán observar las energías del MAS
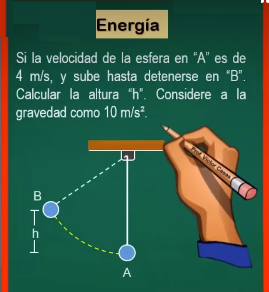
Ejemplos
Una
masa de 10 kilogramos se liga a un resorte
de 0,8 N/m de constante de elasticidad, si se desplaza 10 centímetros
del punto de equilibrio, calcular:
a) Em
total b)
Velocidad máxima c) Epe y Ec
cuando t = T/3
Para hallar el PERÍODO de una masa que oscila
suspendida de un resorte, se hace lo siguiente:
Veamos algunos vídeos donde se observa el movimiento de las partículas en un MAS
Video uno: Definición del MAS
Video dos: Energías en el MAS
lunes, 16 de marzo de 2015
Péndulo simple
Un
péndulo simple consiste en una masa suspendida
de un hilo, que suponemos de masa
despreciable, la cual oscila en
forma periódica.
De la gráfica se observa que al separar el péndulo de su
posición de equilibrio, adquiere energía potencial gravitatoria (Epg) en
B. Al dejarlo libre se inicia el proceso de sustitución de la energía potencial por energía cinética (Ec), hasta llegar al
punto de equilibrio donde toda la energía es cinética. El péndulo continúa su movimiento,
llega al punto de retorno A donde toda la energía es potencial, sigue el
movimiento de A hasta
O, se pierde E potencial gravitatoria y gana
E cinética,
la cual es máxima en el punto O; luego pierde E cinética hasta llegar al punto
B donde toda la energía es potencial
y completa una oscilación, así
continúa en forma periódica.
Veamos una animación del péndulo simple, donde observaremos los vectores fuerza y velocidad
Veamos una animación del péndulo simple, donde observaremos los vectores fuerza y velocidad
Para poder concluir que el movimiento del péndulo
simple es un MAS, se debe verificar
que la fuerza resultante que actúa
sobre él es recuperadora y tiene la
forma:
F = - KX
En la siguiente
figura se puede observar que sobre la masa
m actúan dos fuerzas diferentes, la tensión
T y el peso W.
Por trigonometría
tenemos:
Como la fuerza
es contraria al movimiento, se toma negativa. Sí las amplitudes del péndulo son
muy pequeñas, se tiene que:
Podemos decir entonces que el movimiento del péndulo
simple es periódico y producido por una fuerza recuperadora F = -KX, por lo tanto es
un MAS.
Sabemos que
el período de un MAS está dado por la fórmula:
Veamos un péndulo caótico
Aprovechando todas
las herramientas que nos traen las TIC, y
los recursos didácticos en el proceso ENSEÑANZA
APRENDIZAJE de la física, en las siguientes direcciones
electrónicas podemos encontrar lecturas complementarias
y una serie de animaciones que nos ayudarán a una mejor
comprensión de todo lo relacionando con los movimientos de
los cuerpos en la naturaleza.
Fenómenos naturales y vectores
Fenómenos naturales y vectores
Suscribirse a:
Comentarios (Atom)